| descartes-src (ソースパッケージ descartes-src-0.26.0.tar.gz) | 2012-09-09 20:57 |
| descartes-win (Windows用バイナリパッケージ descartes-win-0.26.0.zip) | 2012-09-09 20:52 |
| 会話キャラクター: ツンデレ アプリケーション (会話キャラ:ツンデレ v1.0 for Windows) | 2010-04-29 13:41 |
| 会話キャラクター: 2人の女の子 ダブルキャラクター (会話キャラクター 2人の女の子 ダブルキャラクター 1.0 for Windows) | 2011-10-02 22:23 |
| 会話キャラクター: Eliza風英語版 (会話キャラ:Eliza風英語版 v1.0 for Windows) | 2010-05-11 01:06 |
| 会話キャラクター: 猫耳メイド アプリケーション (会話キャラ:猫耳メイド v1.0 for Windows) | 2010-04-27 21:15 |
| 会話キャラクター: イライザ風日本語版 (会話キャラ:イライザ風日本語版 v1.0 for Windows) | 2010-04-30 21:53 |
| 経済指標表示プログラム for Windows (経済指標表示プログラム V1.0) | 2011-08-18 22:04 |
| ニュースヘッドライン表示プログラム (ニュースヘッドライン表示プログラム V1.0 for Windows) | 2011-08-16 12:31 |
| デカルト言語 example (デカルト言語の例題 example-0.7.0.zip) | 2009-03-01 19:47 |
| 電力状況表示プログラム for Windows (2011年夏版 全国電力供給状況表示プログラム V1.0) | 2011-08-15 13:25 |
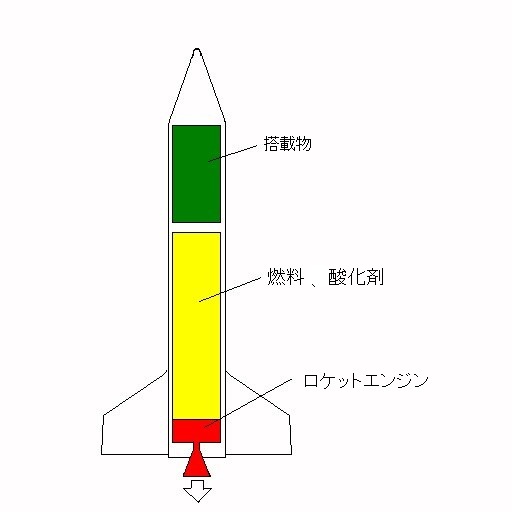
ここでは、上図に示すような1段式のロケットについて、運動方程式を使い、重量、位置、速度、加速度の変化を計算してみましょう。
以下にロケットの運動方程式を示します。
v = Isp * g * log(M / m) dm -- = -1.575 dt
v は、時刻tでの速度です。
Isp は、比推力で主に燃料によって定まる固有の定数です。
ロケット燃料の噴射ガスの平均排気速度です。
g は、重力加速度です。
M は、ロケットの最初の質量で、m は、時刻tでの燃料を使った状態の質量です。
燃料として使用されるので、質量はdm/dt = -1.575で減少していきます。
以下にロケットの運動方程式を数値計算するデカルト言語によるソースを示します。
? ::sys <PrintResultOff>
<letf #g = 9.8>
<letf #M = 375>
<letf #mi = #M>
<letf #Isp = 440>
<letf #xi = 0>
<print "t,x,v,a,m">
::sys <ODE (#t 0 200 0.1)
<letf #'dm/dt' = -1.575>
::sys <integral #m #'dm/dt' #mi>
<letf #v = #Isp * #g * ::sys <log _ <letf _ = #M / #m>>>
::sys <integral #x #v #xi>
::sys <ODEdiff #a #v>
::sys <ODEprintf 100 #t "," #x "," #v "," #a "," #m <\_n>>
>
;
定数として、#Mの質量を初期値375Kg, 非推力440秒としています。
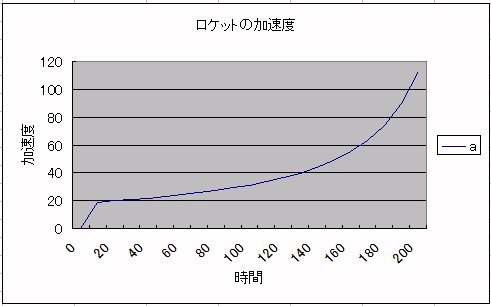
そして、速度#vを計算した後、integral述語で積分することによって位置#xを計算し、 ODEdiff述語で微分することによって加速度#aを計算します。
ソースを"rocket.dec"という名前で保存して実行します。
$ descartes rocket.dec >rocket.csv
rocket.csv を、Excelで読み込んでグラフにしました。
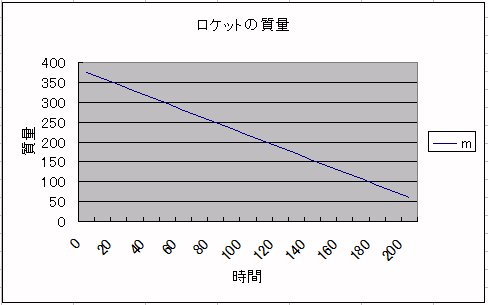
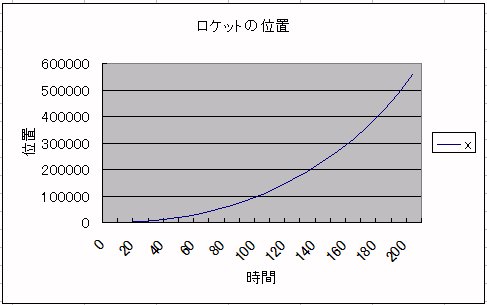
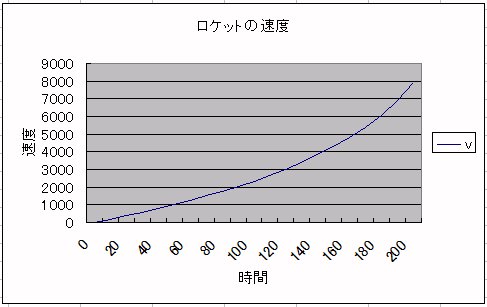
[PageInfo]
LastUpdate: 2012-08-30 22:21:50, ModifiedBy: hniwa
[License]
![]() Creative Commons 2.1 Attribution
Creative Commons 2.1 Attribution
[Permissions]
view:all, edit:login users, delete/config:login users