| descartes-src (ソースパッケージ descartes-src-0.26.0.tar.gz) | 2012-09-09 20:57 |
| descartes-win (Windows用バイナリパッケージ descartes-win-0.26.0.zip) | 2012-09-09 20:52 |
| 会話キャラクター: ツンデレ アプリケーション (会話キャラ:ツンデレ v1.0 for Windows) | 2010-04-29 13:41 |
| 会話キャラクター: 2人の女の子 ダブルキャラクター (会話キャラクター 2人の女の子 ダブルキャラクター 1.0 for Windows) | 2011-10-02 22:23 |
| 会話キャラクター: Eliza風英語版 (会話キャラ:Eliza風英語版 v1.0 for Windows) | 2010-05-11 01:06 |
| 会話キャラクター: 猫耳メイド アプリケーション (会話キャラ:猫耳メイド v1.0 for Windows) | 2010-04-27 21:15 |
| 会話キャラクター: イライザ風日本語版 (会話キャラ:イライザ風日本語版 v1.0 for Windows) | 2010-04-30 21:53 |
| 経済指標表示プログラム for Windows (経済指標表示プログラム V1.0) | 2011-08-18 22:04 |
| ニュースヘッドライン表示プログラム (ニュースヘッドライン表示プログラム V1.0 for Windows) | 2011-08-16 12:31 |
| デカルト言語 example (デカルト言語の例題 example-0.7.0.zip) | 2009-03-01 19:47 |
| 電力状況表示プログラム for Windows (2011年夏版 全国電力供給状況表示プログラム V1.0) | 2011-08-15 13:25 |
空気抵抗がある場合の自由落下運動の微分方程式を以下に示します。
dv -- = -g - B * v dt
gは重力加速度です。 vは落下する物体の速度です。 Bは速度vのときの空気抵抗により変化する加速度のための定数です。
/* 空気抵抗のある自由落下 */
? ::sys <PrintResultOff>
<letf #g = 9.8>
<letf #B = 0.8>
<letf #xi = 100>
<letf #vi = 80>
<setVar var_x #xi>
<setVar var_v #vi>
::sys <ODE (#t 0 11 0.1)
<var_v #v>
<letf #'dv/dt' = - #g - #B * #v>
::sys <integral #v2 #'dv/dt' #vi>
::sys <integral #x2 #v2 #xi>
<printf #t "," #x2 "," #v2 <\_n>>
<setVar var_v #v2>
>
;
まず上記のソースでは定数を設定しています。
#gは、重力加速度gで9.8m/s^2です。
#nは、定数nでここでは0.8とします。
#xiは、位置xの初期値で、100mとします。
#viは、初速で、上方向に80m/sとします。
初期位置#xiは、グローバル変数var_xに設定しています。#xi変数は一度値を設定すると変更できないのでグローバル変数var_xに入れなおすことでODE述語の中で計算途中の値を反映できるようになります。
初速#viは、同様にグローバル変数var_vに設定しておきます。
これで、定数の設定は終わりです。
次にODE述語で微分方程式の計算を行います。ODE述語の引数には、0から11秒後まで0.1秒刻みで変数#tを設定しながら繰り返し実行するように設定します。
ODE述語の中では、対象の微分方程式を数値解析的に計算していきます。
まず、<var_v #v>で、グローバル変数var_vの値を#vに取り出します。
次に<letf #'dv/dt' = - #g - #B * #v>は、前に示した微分方程式を表します。ここで#'dv/dt' となっているのは複雑な外見ではありますが、単なる変数です。#の後ろに'か"で括られた文字列を付けるとそれは変数として解釈されます。
その次の::sys <integral #v2 #'dv/dt' #vi>は、#'dv/dt' を、初期値#viで積分した値を#v2変数に設定します。
ここで#v2には、#tのときの速度が設定されています。
さらに、次に::sys <integral #x2 #v2 #xi>で、初期位置#xiで#v2を積分すると、#tのときの位置#x2が設定されます。
このような積分の計算をODE述語の中で繰り返していくことによって、微分方程式を解いた結果が<printf #t "," #x2 "," #v2 <\_n>>によって表示されていきます。 結果は、","で区切って表示することによって、後に表計算ソフトでCSV形式として使えるようにしておきます。
最後に<setVar var_v #v2>で新たに計算された#v2をグローバル変数var_vに設定します。 速度は、微分方程式<letf #'dv/dt' = - #g - #B * #v>の中で#vとして現れるのでこの値を供給するためにグローバル変数に保持しておくことによって、次のステップの計算で使うことができるようになります。位置#x2については、微分方程式の中には現れないので、グローバル変数に保持する必要はありません。(変数#g, #Bは定数であり値が変化しないので、やはりグローバル変数にする必要はありません。)
このようにODE述語の中ではd~/dtの部分をintegral述語で積分してやることにより、微分方程式の解を求めていくことができます。
ソースをfall.decという名前で保存して実行します。
$ descartes fall.dec 0,100,80 0.1,107.508,72.62 0.2,114.531,65.4368 0.3,120.647,59.0303 0.4,126.349,52.9862 0.5,131.289,47.6061 0.6,135.88,42.5307 0.7,139.832,38.0129 0.8,143.491,33.7509 0.9,146.613,29.9572 1,149.49,26.3783 1.1,151.915,23.1926 1.2,154.134,20.1873 1.3,155.975,17.5122 1.4,157.642,14.9885 1.5,158.991,12.7421 1.6,160.194,10.623 1.7,161.131,8.7366 1.8,161.945,6.95707 1.9,162.535,5.37305 2,163.023,3.87872 2.1,163.322,2.54858 2.2,163.535,1.29375 2.3,163.59,0.176788 ... 途中略 9.9,84.7118,-12.2337 10,83.4884,-12.2351 10.1,82.2648,-12.2363 10.2,81.0412,-12.2375 10.3,79.8173,-12.2385 10.4,78.5935,-12.2395 10.5,77.3695,-12.2404 10.6,76.1454,-12.2412 10.7,74.9212,-12.2419 10.8,73.697,-12.2426 10.9,72.4727,-12.2432 11,71.2484,-12.2438
カンマで区切られた、時間, 位置, 速度がCSV形式で順に出力されます。
以下のように、pai.csvという名前で結果を保存してみましょう。
$ descartes fall.dec > fall.csv
このように保存されたファイルは表計算ソフトで使えます。 Windowsならばfall.csvをダブルクリックしただけでEXCELで開くことができます。
EXCELで読み込んでから、グラフ化したものを次に示しましょう。
(グラフ化する方法は、お持ちの表計算プログラムの方法に従ってください。)
空気抵抗のある場合の落下速度の変化を示します。

だんだんと速度が一定の値になるため、グラフの値が水平になっていきます。
空気抵抗のある場合の落下速度の変化を示します。

位置の変化は、最初は2次曲線だったのが傾いた直線になっていきます。
熱いお湯を室温で放置した場合の冷え方を表す微分方程式を以下に示します。
dT k * s -- = - ------*(T - T0) dt c * m
kは、熱伝達係数で定数です。
Sは、熱が通過する面積です。
Cは、水の比熱で定数です。
mは、お湯の質量です。
Tは、お湯の温度です。
T0は、室温です。
この微分方程式を解いて、時間の経過によって変化していくお湯の温度について見てみましょう。
/* お湯の冷え方 */
? ::sys <PrintResultOff>
<letf #Ti = 98> // 初期値 98度
<setVar var_T #Ti>
<letf #Tnow = 25> // 現在室温
<letf #k = 20> // 定数
<letf #C = 4.2>
<letf #S = 0.2>
<letf #m = 100>
<letf #N = -(#k * #S) / (#C * #m)>
<print "t,T"> // 値名を印刷
::sys <ODE (#t 0 600 1) // 0から 600まで1刻みで繰り返す
<var_T #T> // Tの値を#Tに取り出し
// dT/dtの微分方程式
<letf #'dT/dt' = #N * (#T - #Tnow)>
::sys <integral #T2 #'dT/dt' #Ti> // dT/dtをtで積分
<print #t "," #T2> // 結果を印刷
<setVar var_T #T2> // Tの値を保存
>
;
まず上記のソースでは定数を設定しています。
#Tiは、お湯の温度の初期値です。ここでは98度としています。 それをグローバル変数のvar_tに設定しておきます。
#Tnowは、室温です。でここでは25度とします。
#kは、熱伝達係数の定数で、20とします。
#Sは、熱が通過する面積で、ここでは0.2m2とします。
#Cは、水の比熱の定数で4.2とします。
#mは、お湯の質量で100gとします。
微分方程式の中で、-(#k * #S) / (#C * #m)の部分はすべて定数で構成されているので計算途中で変化することはありません。そのため、この値を事前に計算しておいて、#Nに設定しておきます。
次にODE述語で微分方程式の計算を行います。ODE述語の引数には、0から600秒後まで1秒刻みで変数#tを設定しながら繰り返し実行するように設定します。
ODE述語の中では、対象の微分方程式を数値解析的に計算していきます。
まず、<var_T #T>で、グローバル変数var_Tの現在のお湯の温度の値を#Tに取り出します。
次に<letf #'dT/dt' = #N * (#T - #Tnow)>は、前に示した微分方程式を表します。ここで#'dT/dt' となっているのは単なる変数です。
その次の::sys <integral #T2 #'dT/dt' #Ti>は、#'dT/dt' を、初期値#Tiで積分した値を#T2変数に設定します。
ここで#T2には、時刻#tのときのお湯の温度が設定されています。
このような積分の計算をODE述語の中で繰り返していくことによって、微分方程式を解いた結果が<print #t "," #T2>によって表示されていきます。 結果は、","で区切って表示することによって、後に表計算ソフトでCSV形式として使えるようにしておきましょう。
最後に<setVar var_T #T2>で新たに計算されたお湯の温度#T2をグローバル変数var_Tに設定します。 お湯の温度は、微分方程式<letf #'dT/dt' = #N * (#T - #Tnow)>の中で#Tとして現れるのでこの値を供給するためにグローバル変数に保持しておくことによって、次のステップの計算で使うことができるようになるのです。 #Nと#Tnowの値は定数であり、時刻が進んでも値が変化しないため、いつも同じ値を使います。そのため、グローバル変数に保存する必要はありません。
このようにお湯の温度の冷め方の微分方程式の解として求めることにより、お湯の温度変化を演算しましょう。
ソースをhotwater.decという名前で保存して実行します。
$ descartes hotwater.dec t,T 0 , 98 1 , 97.3048 2 , 96.6117 3 , 95.9275 4 , 95.2477 5 , 94.5765 6 , 93.9096 7 , 93.2512 8 , 92.597 9 , 91.9511 10 , 91.3094 11 , 90.6759 12 , 90.0464 13 , 89.4249 14 , 88.8073 15 , 88.1977 16 , 87.5919 17 , 86.9939 18 , 86.3997 19 , 85.813 20 , 85.2301 21 , 84.6547 22 , 84.0829 23 , 83.5184 24 , 82.9575 25 , 82.4037 26 , 81.8535 27 , 81.3103 28 , 80.7706 ...途中略 590 , 25.2509 591 , 25.2485 592 , 25.2461 593 , 25.2437 594 , 25.2414 595 , 25.2391 596 , 25.2368 597 , 25.2345 598 , 25.2323 599 , 25.2301 600 , 25.2279
最初は98度だったお湯が室温の25度付近まで下がっているのがわかりますね。
以下のように、hotwalter.csvという名前で結果を保存してみましょう。
$ descartes hotwalter.dec > hotwalter.csv
EXCELで読み込んでから、グラフ化したものを次に示しましょう。
(グラフ化する方法は、お持ちの表計算プログラムの方法に従ってください。)
時間の経過によって変化していくお湯の温度の変化を示します。
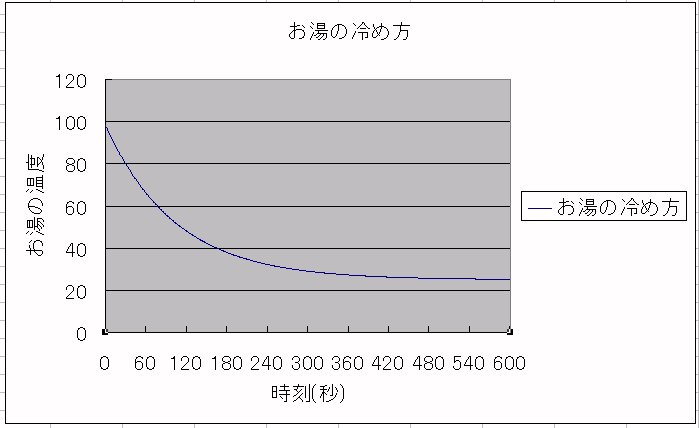
最初は温度が急激に温度が下がっていくのがわかります。 そして、温度が低くなってくると温度の下がり方は緩やかになっていきますね。
実際の感覚的にもこのような温度の下がり方は合っていると感じられます。
最初は熱くて触ることもできないのに、ちょっとすると暖かいくらいになり、その状態が永く続きます。
振り子の運動を表す微分方程式を以下に示します。
今回は振り子の振れ幅の大きい場合の次に示すような非線形の方程式を使います。
2 3 d θ g θ ------ = - - * (θ - -) 2 dt l 6
lは、振り子の長さです。
gは、重力加速度
θは、振り子の振れる角度です。
このような非線形の微分方程式でも、ODE機能を使って解くことが可能です。
/* 振り子の運動 */
? ::sys <PrintResultOff>
<letf #g = 9.8>
<letf #l = 1>
<printf "TIME ,">
::sys <ODE (#t 0 4 0.001)
::sys <ODEprintf 100 #t ",">>
<print>
<foreach (#θi (0.3 0.5 0.8))
<printf "θ=" #θi ",">
<setVar θ #θi>
::sys <ODE (#t 0 4 0.001)
<θ #θ>
<letf #t1 = -#g / #l * (#θ-#θ*#θ*#θ/6)>
::sys <integral #t2 #t1>
::sys <integral #θ2 #t2 #θi>
::sys <ODEprintf 100 #θ2 ",">
<setVar θ #θ2>
>
<print>
>
;
まず上記のソースでは定数を設定しています。
#gは、重力加速度で9.8です。
#lは、振り子の腕の長さです。ここでは1とします。
さて、今回は複数の角度の初期値で振り子の動きを計算するために、出力を横向きに出します。
そこで、まず、時刻TIMEを1行に,で区切った形で出力しています。ここでは、ODE述語を単純な繰り返しとして時刻を出力するために使います。 このときODE述語の引数は後に、微分方程式の演算を行うときと同じ値にしておかなければなりません。
その次の<foreach (#θi (0.3 0.5 0.8))によって、角度(ラジアン)の初期値を0.3, 0.5, 0.8の3種類と指定しています。 この角度の初期値で順に演算していくのですが、今回の微分方程式は非線形であり、初期値の角度により振り子の周期がどのように変化していくのかを見ることが今回の演算の目的です。
次にODE述語で微分方程式の計算を行います。ODE述語の引数には、0から4秒後まで0.001秒刻みで変数#tを設定しながら繰り返し実行するように設定します。 今回の場合のように周期的に振動するようなものの場合には、どうしても誤差が集積しやすいので、細かな刻みで多数の計算を繰り返すようにします。しかし、結果については多数の細かな結果は不要なのでODEprintf文で、一定個数ごとにサンプリングして結果出力するようにします。
ODE述語の中では、対象の微分方程式を数値解析的に計算していきます。
まず、<θ #θ>で、グローバル変数θの現在のお湯の温度の値を#θに取り出します。 θの値は微分方程式の中に現れて、計算結果でどんどん値が変換するためにグローバル変数で保持しておきます。
次に<letf #t1 = -#g / #l * (#θ-#θ*#θ*#θ/6)>は、前に示した微分方程式を表します。
その次の::sys <integral #t2 #t1>と::sys <integral #θ2 #t2 #θi>で2回積分して、新しい振り子の角度#θ2を計算します。
計算結果の#θ2は、::sys <ODEprintf 100 #θ2 ",">により100個おきにカンマで区切って出力します。
最後に<setVar θ #θ2>で新たに計算された角度#θ2をグローバル変数θに設定します。
このようにθを計算することで、振り子の腕の角度の変化を、3通りの初期値(0.3 0.5 0.8)の場合について求めます。
ソースをpendulum.decという名前で保存して実行します。
$ descartes.exe pendulum.dec TIME ,0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2,2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9,3,3.1,3.2,3.3,3.4,3.5,3.6,3.7,3.8,3.9,4, θ=0.3,0.3,0.285629,0.243838,0.17853,0.0958944,0.00387294,-0.0886151,-0.172592,-0.239956,-0.284273,-0.301352,-0.289575,-0.250013,-0.186352,-0.104618,-0.0126544,0.0806288,0.166176,0.235725,0.282632,0.302456,0.293325,0.25606,0.19413,0.113385,0.0215641,-0.0724417,-0.159505,-0.231214,-0.280708,-0.303304,-0.296868,-0.26197,-0.201853,-0.122186,-0.030596,0.064057,0.152582,0.226418,0.278497,0.303888, θ=0.5,0.5,0.476682,0.408712,0.302041,0.16637,0.0144896,-0.138946,-0.279085,-0.392596,-0.469018,-0.501543,-0.487322,-0.427537,-0.327382,-0.195888,-0.0453687,0.1097,0.254292,0.374589,0.459432,0.501223,0.496304,0.445057,0.3519,0.22516,0.0766182,-0.0794982,-0.228059,-0.354806,-0.447908,-0.498977,-0.503538,-0.46116,-0.375467,-0.254054,-0.108116,0.0484378,0.200446,0.333267,0.434425,0.494749, θ=0.8,0.8,0.765169,0.663043,0.501077,0.292376,0.0555617,-0.186858,-0.411526,-0.59762,-0.729256,-0.796283,-0.793941,-0.722342,-0.586489,-0.396816,-0.169511,0.0743424,0.311245,0.518704,0.67825,0.777002,0.807734,0.768304,0.661363,0.494712,0.281872,0.0418929,-0.202373,-0.427414,-0.612475,-0.741889,-0.805786,-0.799678,-0.723928,-0.583812,-0.390094,-0.159348,0.0869784,0.325138,0.532575,0.690935,
横長のCSVの形式で出力されます。
以下のように、pendulum.csvという名前で結果を保存してみましょう。
$ descartes pendulum.dec > pendulum.csv
EXCELで読み込んでから、グラフ化したものを次に示しましょう。
(グラフ化する方法は、お持ちの表計算プログラムの方法に従ってください。)
初期値の角度によって、振り子の周期がどのように変化していくか確認してみましょう。

初期値の角度が大きいほど、周期が長くなっています。
[PageInfo]
LastUpdate: 2012-08-30 22:16:36, ModifiedBy: hniwa
[License]
![]() Creative Commons 2.1 Attribution
Creative Commons 2.1 Attribution
[Permissions]
view:all, edit:login users, delete/config:login users